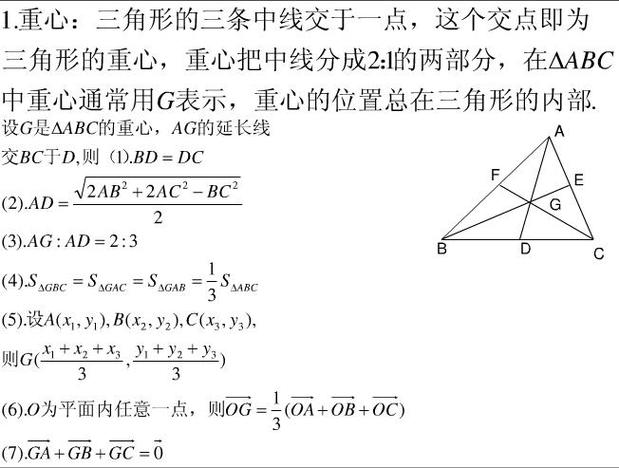
三角形的重心:几何中心的奥秘与计算
在几何学中,三角形是一种基础而重要的图形,它蕴含着丰富的数学性质。其中,三角形的重心是一个尤为关键的概念,它不仅在几何学中占据重要位置,还在物理学、工程学等多个领域有着广泛应用。本文将深入探讨三角形的重心的定义、性质以及计算方法。
一、三角形的重心的定义
三角形的重心,简称三角形的质心,是三角形三条中线的交点。中线是连接三角形任意两边中点的线段。由于三角形有三条边,因此也有三条中线,这三条中线交于一点,这一点就是三角形的重心。
二、三角形的重心的性质
- 重心将中线分为2:1的比例:对于三角形的任意一条中线,重心将该中线分为两段,其中一段是中线的长度,另一段是中线长度的两倍。即,重心到三角形顶点的距离是中线长度的三分之二,而重心到对应边的中点的距离是中线长度的三分之一。
- 重心是三角形内切圆和外接圆的等距点:重心到三角形三个顶点的距离之和最小,等于三角形周长的一半。同时,重心也是三角形内切圆和外接圆的等距点,即重心到内切圆和外接圆的距离相等。
- 重心与三角形的面积关系:三角形的面积可以通过重心和三个顶点构成的三个小三角形的面积之和来计算。具体来说,大三角形的面积等于三个小三角形面积之和的三倍。
三、三角形的重心的计算方法
计算三角形的重心有多种方法,下面介绍两种常用的方法:
1. 坐标法
对于已知三角形三个顶点坐标的情况,可以通过坐标法计算重心的坐标。设三角形三个顶点的坐标分别为(x1, y1)、(x2, y2)、(x3, y3),则重心的坐标(Gx, Gy)可以通过以下公式计算:
Gx = (x1 + x2 + x3) / 3
Gy = (y1 + y2 + y3) / 3
这个公式表明,三角形的重心的坐标是三个顶点坐标的算术平均值。
2. 向量法
向量法是一种更为直观和灵活的计算方法。对于任意三角形ABC,设其重心为G,则可以通过以下步骤计算重心:
- 计算三角形两条边的向量表示,例如AB和AC。
- 计算这两个向量的和向量,即AB + AC。
- 将和向量除以3,得到的结果就是重心G相对于顶点A的位置向量。
- 最后,将位置向量加到顶点A的坐标上,即可得到重心的坐标。
四、三角形的重心的应用
三角形的重心在多个领域有着广泛的应用。在物理学中,重心是物体平衡的关键点,对于静态平衡和动态平衡的分析至关重要。在工程学中,重心的位置对于结构的设计和分析具有重要意义,它影响着结构的稳定性和承载能力。此外,在计算机图形学、机器人学等领域,三角形的重心也有着重要的应用。
总之,三角形的重心是一个充满奥秘和实用价值的几何概念。通过深入理解其定义、性质和计算方法,我们可以更好地应用这一概念解决实际问题。