度和弧度的换算:全面解析与应用
在数学、物理学以及工程学等领域中,角度的度量是一个基础且重要的概念。角度的度量单位主要有两种:度和弧度。虽然它们都能用来表示角的大小,但在不同的应用场景下,各有其独特的优势。本文将详细解析度和弧度之间的换算关系,并探讨它们在实际应用中的差异。
一、度与弧度的基本概念
度(°)是我们日常生活中最为熟悉的角度单位,一个完整的圆周被划分为360度。度是一种直观且易于理解的单位,广泛应用于地理、建筑等领域。
弧度(rad)则是数学和物理学中更为常用的角度单位。一个完整的圆周对应的弧度值为2π(约等于6.2832)。弧度单位使得许多数学公式和物理定律的表达更加简洁和统一。
二、度与弧度的换算公式
度和弧度之间的换算关系可以通过以下公式来表示:
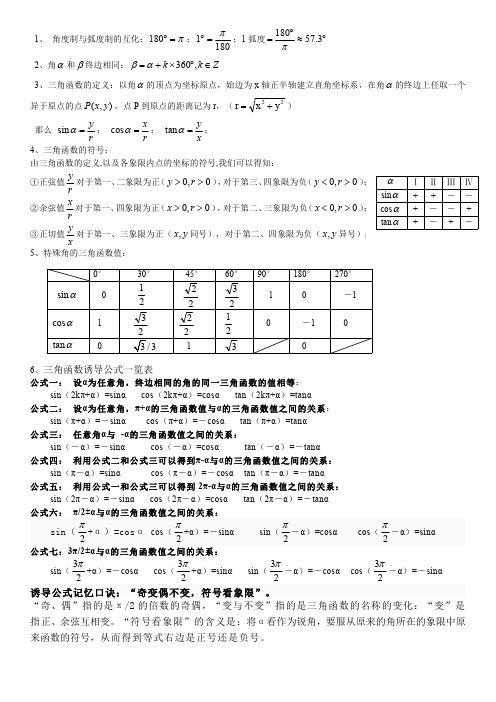
- 将度转换为弧度:弧度 = 度 × (π/180)
- 将弧度转换为度:度 = 弧度 × (180/π)
这两个公式是实现度和弧度相互转换的基础。通过这两个公式,我们可以轻松地将一个角度值从一种单位转换为另一种单位。
三、换算示例
为了更好地理解换算过程,下面给出几个具体的换算示例:
- 示例一:将90度转换为弧度。
弧度 = 90 × (π/180) = π/2 ≈ 1.5708 - 示例二:将π/3弧度转换为度。
度 = (π/3) × (180/π) = 60 - 示例三:将300度转换为弧度。
弧度 = 300 × (π/180) = 5π/3 ≈ 5.2359
四、度与弧度的应用差异
虽然度和弧度都能用来表示角的大小,但它们在实际应用中存在一些差异:
- 数学与物理学:在微积分、三角函数等数学领域以及物理学中,弧度单位更为常用。这是因为弧度单位使得许多公式和定理的表达更加简洁和统一。
- 日常生活与工程应用:在地理、建筑、机械等日常生活和工程应用领域中,度单位更为直观和易于理解。例如,在描述地理位置时,我们通常使用度来表示经纬度。
五、总结
度和弧度是两种常用的角度度量单位,它们各有其独特的优势和应用场景。通过掌握度和弧度之间的换算关系,我们可以更加灵活地处理与角度相关的计算问题。无论是在数学、物理学等理论领域,还是在日常生活、工程应用等实践领域,准确理解和运用这两种角度单位都至关重要。
角度的度量是数学和物理学中的基础概念,掌握度和弧度之间的换算关系对于深入理解和应用相关知识具有重要意义。