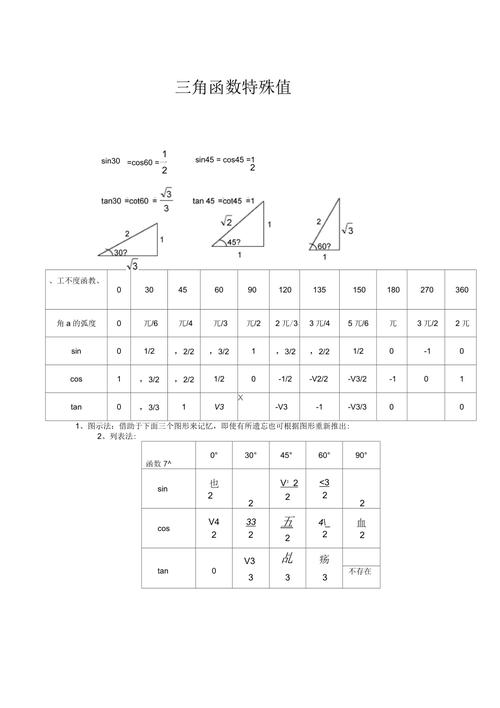
特殊角的三角函数值:探索数学之美
在三角学中,特殊角的三角函数值扮演着至关重要的角色。这些特殊角包括0°、30°、45°、60°和90°,它们的三角函数值不仅在数学中有广泛应用,也是物理学、工程学等多个领域的基础。本文将详细探讨这些特殊角的三角函数值,并深入解析其背后的数学原理。
一、特殊角的定义
在直角坐标系中,特殊角通常指的是与坐标轴成特定角度的射线。这些角度包括:
- 0°:与x轴正方向重合
- 30°:与x轴正方向成30度角
- 45°:与x轴正方向成45度角,即等腰直角三角形的锐角
- 60°:与x轴正方向成60度角
- 90°:与x轴正方向垂直,即y轴正方向
二、特殊角的三角函数值
三角函数包括正弦(sin)、余弦(cos)和正切(tan),它们在特殊角上的值具有特殊的意义和简洁的表达式。
1. 0°
- sin 0° = 0
- cos 0° = 1
- tan 0° = 0
解释:在0°时,射线与x轴重合,y坐标为0,因此正弦值为0;x坐标为1,余弦值为1;正切值为正弦除以余弦,即0/1=0。
2. 30°
- sin 30° = 1/2
- cos 30° = √3/2
- tan 30° = √3/3
解释:在30°的直角三角形中,对边长度为斜边长度的一半,邻边长度为斜边长度的√3/2倍,因此正弦值为1/2,余弦值为√3/2,正切值为对边除以邻边,即1/2 ÷ √3/2 = √3/3。
3. 45°
- sin 45° = √2/2
- cos 45° = √2/2
- tan 45° = 1
解释:在45°的等腰直角三角形中,对边和邻边长度相等,均为斜边长度的√2/2倍,因此正弦和余弦值均为√2/2,正切值为对边除以邻边,即√2/2 ÷ √2/2 = 1。
4. 60°
- sin 60° = √3/2
- cos 60° = 1/2
- tan 60° = √3
解释:在60°的直角三角形中,对边长度为斜边长度的√3/2倍,邻边长度为斜边长度的一半,因此正弦值为√3/2,余弦值为1/2,正切值为对边除以邻边,即√3/2 ÷ 1/2 = √3。
5. 90°
- sin 90° = 1
- cos 90° = 0
- tan 90° 无定义(因为分母为0)
解释:在90°时,射线与y轴重合,x坐标为0,因此余弦值为0;y坐标为1,正弦值为1;正切值为正弦除以余弦,但此时余弦值为0,因此正切值无定义。
三、特殊角三角函数值的应用
特殊角的三角函数值在解决各种实际问题中发挥着重要作用。例如,在物理学中,它们用于描述简谐振动、波动等现象;在工程学中,它们用于计算结构稳定性、材料强度等问题。此外,在导航、测绘、建筑设计等领域,特殊角的三角函数值也是不可或缺的工具。
四、结语
特殊角的三角函数值是三角学中的基石,它们不仅具有简洁而美丽的数学表达式,而且在各个领域都有广泛的应用。通过深入理解和掌握这些特殊角的三角函数值,我们可以更好地运用数学知识解决实际问题,探索自然界的奥秘。
数学之美,在于其简洁与和谐。特殊角的三角函数值,正是这一美的体现。