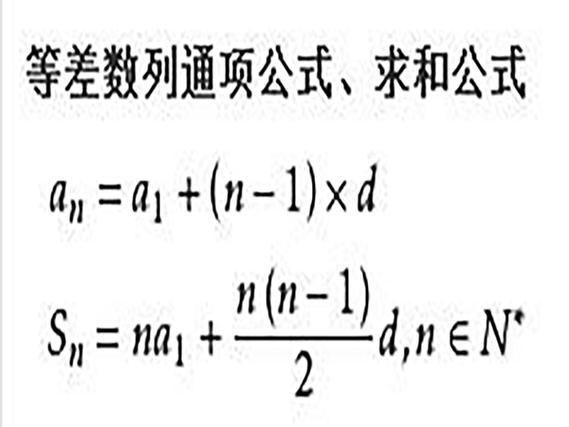等差数列的前n项和公式:探索数学之美与应用之妙
在数学的世界里,等差数列是一种简单而又充满魅力的数列。它以其独特的规律性和广泛的应用性,成为数学学习和研究中的重要内容。本文将深入探讨等差数列的前n项和公式,不仅揭示其背后的数学原理,还将展示这一公式在实际问题中的应用与拓展。
等差数列的基本概念
等差数列,顾名思义,是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列。这个常数被称为公差,通常用字母d表示。等差数列的通项公式为:an = a1 + (n – 1)d,其中a1是首项,n是项数。
等差数列的前n项和公式
等差数列的前n项和公式是数学中的一个重要定理,它给出了等差数列前n项和的计算方法。公式为:Sn = n/2 * (2a1 + (n – 1)d),或者等价地表示为:Sn = n/2 * (a1 + an),其中Sn表示前n项和,a1是首项,an是第n项,d是公差。
公式的推导过程
为了更深入地理解这个公式,我们可以从等差数列的性质出发进行推导。考虑等差数列的前n项,我们可以将其倒序排列,然后与原数列相加,得到:
Sn + Sn = (a1 + a2 + … + an) + (an + an-1 + … + a1) = n(a1 + an)
由于等差数列的性质,每一对相对应的项之和都是相等的,即a1 + an = a2 + an-1 = …。因此,上式可以简化为:
2Sn = n(a1 + an)
进一步整理,得到等差数列的前n项和公式:
Sn = n/2 * (a1 + an)
公式的应用实例
等差数列的前n项和公式在实际生活中有着广泛的应用。以下是一些具体的实例:
- 存款计算:假设某人每月存入银行固定金额,且银行利率固定,那么经过n个月后,该人在银行的存款总额就可以通过等差数列的前n项和公式来计算。
- 工资增长:如果某人的工资每年按固定比例增长,那么经过n年后,该人的累计工资总额同样可以通过等差数列的前n项和公式来估算。
- 物理问题:在物理学中,等差数列的前n项和公式也可以用来解决一些与速度、位移等相关的问题。
公式的拓展与变形
除了基本的等差数列前n项和公式外,我们还可以通过一些变形和拓展,得到更加灵活和实用的公式。例如,当知道等差数列的首项、末项和项数时,可以直接使用公式Sn = n/2 * (a1 + an)来计算前n项和。而当知道首项、公差和项数时,则可以先求出末项an = a1 + (n – 1)d,再代入公式计算。
高级应用:等差数列求和的递推关系
此外,等差数列的前n项和还满足一定的递推关系。即,对于任意的正整数n,都有Sn – Sn-1 = an(n ≥ 2)。这一性质在解决一些复杂的数列问题时非常有用。
结语
等差数列的前n项和公式是数学中的一个基本而重要的定理。它不仅揭示了等差数列求和的内在规律,还为解决实际问题提供了有力的工具。通过深入学习和理解这一公式,我们可以更好地把握数学的本质和魅力,为未来的学习和研究打下坚实的基础。