arctanx图像：深入解析与特性探讨

arctanx图像：深入解析与特性探讨

在数学和工程领域，反正切函数（arctanx）是一个重要的工具，它用于计算一个数的反正切值。arctanx的图像不仅展示了函数的基本形状和性质，还揭示了其在不同领域中的广泛应用。本文将详细探讨arctanx图像的特点、性质以及在实际问题中的应用。

arctanx图像的基本形状

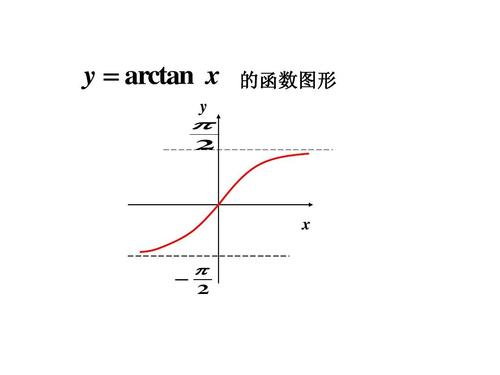
arctanx的图像是一个典型的S形曲线，它关于原点对称。具体来说，当x从负无穷增大到正无穷时，arctanx的值从-π/2逐渐增加到π/2。这种S形曲线在数学上被称为“反S形”或“Sigmoid函数”，它在许多领域都有广泛的应用。

图像的关键点

• 原点：在x=0处，arctanx=0，图像通过原点。
• 渐近线：当x趋近于负无穷时，arctanx趋近于-π/2；当x趋近于正无穷时，arctanx趋近于π/2。因此，图像有两条水平渐近线，分别是y=-π/2和y=π/2。
• 单调性：在(-∞, 0)区间内，arctanx是增函数；在(0, +∞)区间内，arctanx也是增函数。但由于其值域限制在(-π/2, π/2)之间，所以整个函数在其定义域内都是单调递增的。

arctanx图像的几何意义

从几何角度来看，arctanx表示一个角θ的正切值为x时，该角θ的弧度值。换句话说，如果我们在直角坐标系中绘制一条斜率为x的直线，并找到这条直线与单位圆（半径为1的圆）的交点，那么arctanx就是该交点与x轴正方向之间的夹角θ。

arctanx图像的应用

arctanx图像在多个领域都有重要的应用，包括但不限于：

1. 三角函数的反问题

在解决三角函数的反问题时，arctanx是一个非常有用的工具。例如，如果我们知道一个角的正切值，但不知道这个角本身，就可以使用arctanx来找到这个角。

2. 机器学习与神经网络

在机器学习和神经网络中，Sigmoid函数（包括arctanx）常被用作激活函数。这是因为它们能够将输入值压缩到一个有限的范围内（对于arctanx来说是(-π/2, π/2)），从而有助于网络的训练和优化。

3. 物理学与工程学

在物理学和工程学中，arctanx图像经常出现在各种公式和模型中。例如，在电路分析中，arctanx可以用于计算某些类型的阻抗；在力学中，它可以用于描述某些类型的运动轨迹。

结论

arctanx图像是一个具有独特形状和性质的函数图像，它在数学、物理、工程以及机器学习等多个领域都有广泛的应用。通过深入理解arctanx图像的特点和性质，我们可以更好地利用这一工具来解决实际问题。

“arctanx图像不仅是数学中的一个基本概念，更是连接不同学科领域的桥梁。”